二叉树

前言：之前临近期末实在没精力写博客了 :face_with_head_bandage: (原谅我吧），最近把随想录的算法题再整理一下。

二叉树的层序遍历

二叉树的层序遍历在我印象中就是按照每层从左到右一个一个遍历过去，这里的输入是一个包含空的数组，输出则是一个二维数组，其中的元素表示每层。

102.二叉树的层序遍历

输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

这里的输入只是一个示意，实际输入的是一个根节点

每行的数组长度是不确定的，所以我打算采用ArrayList的add方法动态增加元素

搜索同一层结点的时候就是关键

先用最容易想到的方法，访问一层第n中的每个节点都从根节点开始，访问n次

/**
 * 输入当前子树的根节点和树高n，将子树的n高的节点的值存入ArrayList中
 * @param cur
 * @param n
 * @param list
 */
public void addList(TreeNode cur, int n, ArrayList<Integer> list) {
    if(n == 1) {
        list.add(cur.val);
        return;
    }
    if(cur.left != null) {
        addList(cur.left, n-1, list);
    }
    if(cur.right != null) {
        addList(cur.right, n-1, list);
    }
}

这个方法可以将第n层的所有值存入ArrayList中

那么还有一个问题：如何确定n（树的高度）的大小？

/**
 * 求出树的高度,需要输入n=1
 * @param root
 * @param n
 * @return
 */
public int countTreeHowHigh(TreeNode root ,int n) {
    int left = 0;
    int right = 0;
    if(root.left != null) {
        left = countTreeHowHigh(root.left, n+1);
    }
    if(root.right != null) {
        right = countTreeHowHigh(root.right, n+1);
    }
    return max(max(left, right), n);
}

验证是通过的，不过递归和栈相似的先进后出的逻辑比较适用于深度搜索，对于层序遍历这种广度搜索可想而知计算复杂度达到了惊人的

image-20250705141727588

接下来看看更好的解法，用队列，先进先出。首先先将根节点放入队列，然后将根节点的左右节点分别放入队列，接着将根节点弹出，剩下的就是第二层的节点了，之后进行一样的操作，就可以实现层序遍历了。这里巧妙地执行一种操作实现了功能，但和递归还是有些不同，更接近迭代。

ArrayList不适合作为队列，采用LinkedList

public List<List<Integer>> levelOrder(TreeNode root) {
    ArrayList<List<Integer>> res = new ArrayList<>();
    LinkedList<TreeNode> list = new LinkedList<>(); // 队列
    list.add(root);
    while(!list.isEmpty()) {
        ArrayList<Integer> layer = new ArrayList<>();
        for(TreeNode node : list) {
            if(node.left != null) {
                list.add(node.left);
            }
            if(node.right != null) {
                list.add(node.right);
            }
            layer.add(list.pop().val);
        }
        res.add(layer);
    }
    return res;
}

按照队列的思路，我写了以上代码，但是运行的时候报错了

Exception in thread "main" java.util.ConcurrentModificationException
	at java.base/java.util.LinkedList$ListItr.checkForComodification(LinkedList.java:977)
	at java.base/java.util.LinkedList$ListItr.next(LinkedList.java:899)
	at Test1.Solution2.Solution.levelOrder(Main.java:36)
	at Test1.Solution2.Main.main(Main.java:18)

并发修改异常ConcurrentModificationException，说是在使用迭代器遍历（for-each循环）时我修改了集合

为什么要设置这个保护机制?

使用ListIterator

最后的代码

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        ArrayList<List<Integer>> res = new ArrayList<>();
        if(root == null) {
            return res;
        }
        Queue<TreeNode> queue = new LinkedList<>(); // 队列
        queue.offer(root);
        while(!queue.isEmpty()) {
            List<Integer> layer = new ArrayList<>();
            int size = queue.size();
            for(int i = 0; i < size; i++) {
                TreeNode node = queue.poll();
                if(node != null) {
                    layer.add(node.val);
                    if (node.left != null) {
                        queue.offer(node.left);
                    }
                    if (node.right != null) {
                        queue.offer(node.right);
                    }
                }
            }
            res.add(layer);
        }
        return res;
    }
}

image-20250705152518367

not bad

参考代码

class Solution {
    public List<List<Integer>> resList = new ArrayList<List<Integer>>();

    public List<List<Integer>> levelOrder(TreeNode root) {
        //checkFun01(root,0);
        checkFun02(root);

        return resList;
    }

    //BFS--递归方式
    public void checkFun01(TreeNode node, Integer deep) {
        if (node == null) return;
        deep++;

        if (resList.size() < deep) {
            //当层级增加时，list的Item也增加，利用list的索引值进行层级界定
            List<Integer> item = new ArrayList<Integer>();
            resList.add(item);
        }
        resList.get(deep - 1).add(node.val);

        checkFun01(node.left, deep);
        checkFun01(node.right, deep);
    }

    //BFS--迭代方式--借助队列
    public void checkFun02(TreeNode node) {
        if (node == null) return;
        Queue<TreeNode> que = new LinkedList<TreeNode>();
        que.offer(node);

        while (!que.isEmpty()) {
            List<Integer> itemList = new ArrayList<Integer>();
            int len = que.size();

            while (len > 0) {
                TreeNode tmpNode = que.poll();
                itemList.add(tmpNode.val);

                if (tmpNode.left != null) que.offer(tmpNode.left);
                if (tmpNode.right != null) que.offer(tmpNode.right);
                len--;
            }

            resList.add(itemList);
        }

    }
}

发现也是可以用递归做的，是要事先将结果中几层的结构先搭建好，对号入座，即使是在深度搜索，也不会导致顺序错乱。队列的方法差不多，类的选取也一致。

一般在IDEA中进行调试，Java中在一个包中的类名不能重复，所以为了方便起见，把每题放在不同包里

翻转二叉树

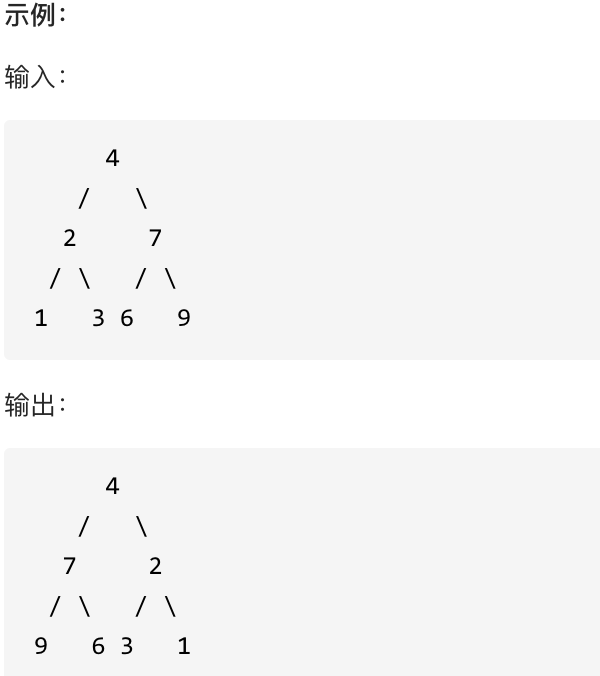
226.翻转二叉树

如图。这道题目比较简单，但还是有需要注意的地方。

首先想到的还是递归（某人还真是喜欢递归）

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null) {
            return root;
        }
        TreeNode temp = root.right;
        root.right = root.left;
        root.left = temp;
        if(root.left != null) {
            invertTree(root.left);
        }
        if(root.right != null) {
            invertTree(root.right);
        }
        return root;
    }
}

image-20250708200404835

我这种递归是何种遍历方式呢？前序遍历。不过不管什么顺序貌似都没问题，吗？

想要实现二叉树的翻转，对于每个节点都需要进行一次左右子节点翻转（准确来说是奇数次翻转），那么前序遍历和后序遍历都可以，理论上中序遍历也是遍历每一个节点，应该没问题，但是实际会出现偏差，中序遍历是左根右，当我们找右子树时中间已经经历了一次翻转，此时我们找到的实际上是左子树，也就是左子树重复翻转了两次，而右子树实际一直没有访问到。

真想要中序遍历的话也是可行的，只是代码需要别扭一些。

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null) {
            return root;
        }
        if(root.left != null) {
            invertTree(root.left);
        }
        TreeNode temp = root.right;
        root.right = root.left;
        root.left = temp;
        if(root.left != null) {
            invertTree(root.left);
        }
        return root;
    }
}

发现代码可以写得再简单一些，不过少了一些剪枝，内存消耗会多一些就是了。

class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null) {
            return root;
        }
        TreeNode temp = root.right;
        root.right = root.left;
        root.left = temp;
        invertTree(root.left);
        invertTree(root.right);
        return root;
    }
}

image-20250708203829237

tips:递归三部曲

1.确定参数和返回

2.确定边界条件/终止条件

3.确定递归逻辑

既然我们知道了翻转就等价于遍历每个节点的翻转其子树，那么问题就转化为遍历一遍节点的方法了，用迭代的方法肯定也能做，这就可以用我们之前的统一迭代法

对称二叉树

包装类

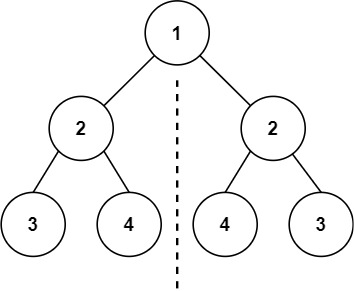
判断二叉树是否对称。

img

img

第一种想法，比较对称的两种前序遍历，每个节点一一比较。

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root == null || root.left == null && root.right == null) {
            return true;
        }
        Stack<TreeNode> st1 = new Stack<>();
        Stack<TreeNode> st2 = new Stack<>();
        st1.push(root);
        st2.push(root);
        while(!(st1.isEmpty() && st2.isEmpty())) {
            TreeNode node1 = st1.pop();
            TreeNode node2 = st2.pop();
            if(node1.val != node2.val) {
                return false;
            }
            if(node1.left != null && node2.right != null) {
                st1.push(node1.left);
                st2.push(node2.right);
            } else if (!(node1.left == null && node2.right == null)) {
                return false;
            }
            if(node1.right != null && node2.left != null) {
                st1.push(node1.right);
                st2.push(node2.left);
            } else if (!(node1.right == null && node2.left == null)) {
                return false;
            }
        }
        return true;
    }
}

image-20250710143824022

第二种想法，对比对称的两种层序遍历的结果，判断是否相同。

我先尝试用左右对称的层序遍历，貌似没那么简单，因为TreeNode中的val是int类型而非Integer类型，所以无法直接创建值为null的节点，会无法判断上图的第二种情况，就算将null节点存储为一个特殊值（比如-1），那么所有null就会一直延申下去，造成死循环。

public class TreeNode {
    public int val;
    public TreeNode left;
    public TreeNode right;
    public TreeNode() {}
    public TreeNode(int val) { this.val = val; }
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

如何突破？可以从这个切入点入手——“无法直接创建值为null的节点”。既然无法直接创建值为null的节点，那么我就将TreeNode类包装一下，使其能应对值为null的情况。

class TreeNodePlus {
    public Integer val;
    public TreeNode left;
    public TreeNode right;
    TreeNodePlus(TreeNode node){
        if(node != null) {
            this.val = node.val;
            this.left = node.left;
            this.right = node.right;
        } else {
            this.val = null;
            this.left = null;
            this.right = null;
        }
    }
}

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root == null || root.left ==null && root.right == null) {
            return true;
        }
        ArrayList<Integer> ans_l = new ArrayList<>();
        Queue<TreeNodePlus> list_l = new LinkedList<>();
        list_l.add(new TreeNodePlus(root));
        while(!list_l.isEmpty()) {
            TreeNodePlus node = list_l.poll();
            if(node != null) {
                ans_l.add(node.val);
            }
            if(node.val != null) {
                list_l.add(new TreeNodePlus(node.left));
                list_l.add(new TreeNodePlus(node.right));
            }
        }
        ArrayList<Integer> ans_r = new ArrayList<>();
        Queue<TreeNodePlus> list_r = new LinkedList<>();
        list_r.add(new TreeNodePlus(root));
        while(!list_r.isEmpty()) {
            TreeNodePlus node = list_r.poll();
            if(node != null) {
                ans_r.add(node.val);
            }
            if(node.val != null) {
                list_r.add(new TreeNodePlus(node.right));
                list_r.add(new TreeNodePlus(node.left));
            }
        }
        return ans_l.equals(ans_r);
    }
}

通过是通过了，不过因为包装类用时来到了可怕的

image-20250709115859697

第三种想法，通过上节的翻转二叉树来说，反转过后的二叉树如果完全相同那么就是对称的，比较对称的两种前序遍历，我觉得是一种思路，不过比起直接遍历比较净多了翻转的步骤，当然是效率不高的。前序遍历和后序遍历是无法区分只有单左子树和单右子树的，所以在这里不行，那么中序遍历是可以区分的。

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root == null || root.left == null && root.right == null) {
            return true;
        }
        Stack<TreeNode> st1 = new Stack<>();
        ArrayList<Integer> res1 = new ArrayList<>();
        st1.push(root);
        while(!st1.isEmpty()) {
            TreeNode node = st1.pop();
            if(node == null) {
                node = st1.pop();
                res1.add(node.val);
                System.out.println(node.val);
                continue;
            }
            if(node.right != null) {
                st1.push(node.right);
            }
            st1.push(node);
            st1.push(null);
            if(node.left != null) {
                st1.push(node.left);
            }
        }

        // 翻转二叉树
        Stack<TreeNode> st = new Stack<>();
        st.push(root);
        while(!st.isEmpty()) {
            TreeNode node = st.pop();
            TreeNode temp = node.left;
            node.left = node.right;
            node.right = temp;
            if(node.left != null) {
                st.push(node.left);
            }
            if(node.right != null) {
                st.push(node.right);
            }
        }

        Stack<TreeNode> st2 = new Stack<>();
        ArrayList<Integer> res2 = new ArrayList<>();
        st2.push(root);
        while(!st2.isEmpty()) {
            TreeNode node = st2.pop();
            if(node == null) {
                node = st2.pop();
                res2.add(node.val);
                System.out.println(node.val);
                continue;
            }
            if(node.right != null) {
                st2.push(node.right);
            }
            st2.push(node);
            st2.push(null);
            if(node.left != null) {
                st2.push(node.left);
            }
        }
        return res1.equals(res2);
    }
}

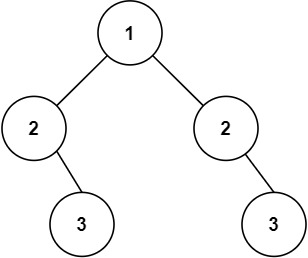
采用中序遍历，就没问题了吗？还有问题，当root =[1,2,2,2,null,2]的时候还是无法区分，相同值会造成干扰，那么还是得在遍历的每次中都比较才行。这就把翻转二叉树的方案基本推翻了，因为翻转改变了二叉树的结构导致两次遍历必须先后进行，要么就在翻转的时候新建一颗树，那太离谱了，就不考虑了。这种方法和第一种方法的区别主要在于第一种方法是每个节点一一对应比较的，能够应对空节点的情况，而第三种方法比较的是翻转前后的遍历结果，会有很多树的结构不同但是遍历结果相同的结果来混淆。

参考链接：

【代码随想录】https://www.programmercarl.com/0102.%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E5%B1%82%E5%BA%8F%E9%81%8D%E5%8E%86.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE